線形代数学の理解がグングン進むポイント（画像あり）

理系の大学生が１年生に学ぶのが「線形代数学」です。
今回は、その線形代数学を理解しやすくするポイントをいくつか紹介します。
いずれも私が大学１年生のときに、ぜひ知りたかった、
けれども誰も教えてくれなかった内容です。

線形代数学とは何か？

一言で言えば、線形代数学は「行列とベクトルの学問」です。

言葉の意味から説明しましょう。

「代数」とは「数の代わり」と書くように、
数字の代わりに文字を使って式を書くときに「代数」という言葉を使います。

たとえば
$3+5=8$
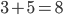
という式は、普通の数字を使った式です。
対して
$(a+b)^2 = a^2 + 2ab + b^2$
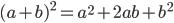
という式は、aやbといった文字を使った式ですので「代数式」と呼ばれます。
代数を使うことにより、一般的な法則を導き出すことができます。

続いて「線形」とは、「１次」ということです。
たとえば
$a+b$
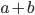
は１次式ですが、
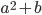$a^2+b$や　$ab+cd$
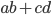
のように２つ以上の代数がかけられているものは２次式です。

線形代数学と行列・ベクトルの関係

さらに線形代数を学ぶ上で、次の対応を頭に入れていると理解がしやすいと思います。

線形代数学と行列・ベクトルの関係

線形代数で出てくる言葉	高校までに習った言葉
写像	関数
１次写像	行列
元	ベクトル

写像とは「ある元を別の元に写すもの」と定義されます。

ｍ行ｎ列の行列は、ｎ次元ベクトルをｍ次元ベクトルに写す写像となります。

また実際、１次写像の定義を行列が満たすことは簡単にチェックできるでしょう。

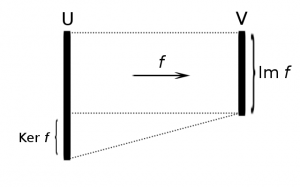
像(Image)・核（Kernel）のイメージ

線形代数をやっていて、多くの大学生がとまどうのが
像(Image, Im)や核（Kernel, Ker）のイメージがわかないことでしょう。

しかし、次の図を見れば一発で分かるはず。

ちなみに像の次元 dim Im f を rank f と表記しますが、
これは写像fを行列とみなしたときの、行列の階数（rank）と一致します。

線形代数は何の役に立つのか？

「線形代数って何の役に立つんだ？」と思う大学生は多いはず。

しかし学年が上がると、線形代数は理系の学問の基礎になっていることが分かると思います。

たとえば数学であれば、代数学・幾何学・解析学のいずれにおいても線形代数が基礎となっていますし
物理でも量子力学をまじめにやろうと思えば、線形代数の知識は必須です。

電気工学系や情報工学においても線形代数の知識が必要となってきます。

モチベーションをあげてがんばっていきましょう(^-^)/